
CRYPTAGE ASYMETRIQUE
Un moyen de crypter infaillible
I) Qu’est-ce que le cryptage asymétrique ?
Le système de cryptage asymétrique est un moyen puissant de chiffrer des données personnelles. Aujourd'hui, il nous entoure sans même que nous le sachions. Il est dans nos cartes bancaires, nos transactions, nos messageries, nos logiciels... Bref partout !
Ce système a été inventé en 1977 par trois mathématiciens : Ron Rivest, Adi Shamir et Len Adleman d’où l’acronyme RSA, la première lettre de leurs noms.
En chiffrement il existe deux moyens majeurs de coder, le cryptage symétrique qui utilise la même clé pour coder et décoder, et le cryptage asymétrique qui utilise deux clés, une pour coder et l’autre pour déchiffrer. Pour comparer simplement, en cryptage symétrique, vous prenez un coffre, vous le fermez avec une clé x puis vous l'envoyez au destinataire qui l'ouvrira avec la même clé x. Avec le cryptage asymétrique, votre destinataire mettrait des coffres ouverts à disposition de tous, vous mettez votre message dedans puis le fermez à l'aide de la clé x fournit avec, qui est la même pour tous. Désormais seul votre destinataire sera en mesure de l'ouvrir avec sa clé y qui n'ouvre que ses coffres.
Pour le cryptage asymétrique on appellera clé publique celle qui sert à fermer le coffre et clé privée celle qui sert à l’ouvrir. La clé publique est à disposition dans un annuaire, la clé privée elle ne doit être connue que de son propriétaire, il ne doit en aucun cas la transmettre à quelqu’un d’autre car cette personne serait alors en mesure de déchiffrer les messages qui ne lui sont pas destinés.
Nous utiliserons les personnages emblématiques de la cryptographie c’est-à-dire Alice et Bob (A et B).
Alice veut communiquer un message à Bob, elle prend donc la clé publique de Bob et crypte son message avec. Une fois crypté, Alice ne peut plus le décrypter avec la clé publique de Bob. Lui seul sera en mesure de le déchiffrer avec sa clé privée.
L’avantage d’un tel système est que tout le monde pourra envoyer des messages à Bob et Bob sera le seul à pouvoir les comprendre; De plus il n’y a pas besoin d’envoyer une clé secrète qui pourrait être interceptée pendant cette opération. Autre point clé : ce système utilise des fonctions à sens uniques qui sont simples à appliquer mais rendent l’opération inverse extrêmement compliquée sans une aide extérieure, c’est-à-dire la clé privée.
II) Créez votre propre système de chiffrement asymétrique :
Armez-vous d’une feuille, d’une calculette, et de courage.
Tout d’abord pour créer la clé publique vous devrez choisir deux nombres premiers que l’on appellera P et Q
On choisira ici P= 79 et Q= 41
Vous allez multiplier ces nombres entre eux et obtenir N
N= P*Q= 79*41=3239
Ensuite nous devons obtenir M= (P-1)*(Q-1) Ce nombre est l’indicatrice d’Euler, Il permet de connaître le nombre d’entier naturels qui sont inférieurs ou égaux à N et qui lui sont premiers
M= (79-1)*(41-1)= 3120
Nous devons maintenant obtenir C qui sera premier avec M
C=7 (par exemple)
Voici la clé publique ( C , N )
Ici ( 7 , 3239 )
Passons maintenant à la clé privée, celle que vous seul devez connaître. Nous allons tout d’abord calculer U qui sera la clé d’inversement de cette fonction. Nous allons chercher U à l'aide de l'identité de Bachet-Bezout qui affirme que : C*U + M*V = 1 uniquement si C et M sont premiers entre eux; ce qui est le cas ici
Pour déterminer U un algorithme est à votre disposition ici (tuxweb79.free.fr/Bezout_win.zip)
Ici on trouve U = 1783
(Une fois le logiciel téléchargé ouvrez son dossier puis appuyez sur clique droit et majuscule, une fenêtre de contrôle va s'ouvrir, tapez ensuite « Bezout.exe » et insérez C et M puis appuyez sur entrée ; ATTENTION si le résultat affiché est négatif l’algorithme ne fonctionnera pas ; pour y remédier écrivez « -rsa » devant C et M)
Nous avons désormais notre clé privée ( U , N )
Donc ( 1783 , 3239 )
III) Apprenez à utiliser la clé de cryptage publique :
La première étape consistera à transformer votre messages en valeurs numériques, pour cela nous allons utiliser la table caractères ASCII ( plus de caractères ici ).
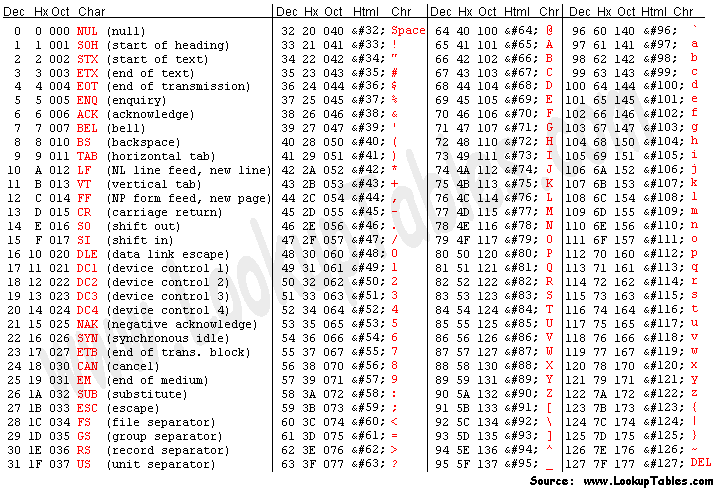
Imaginons que le message que Alice veut envoyer à Bob soit : " Need help! "
N ⇒ 78
e ⇒ 101
e ⇒ 101
d ⇒ 100
"espace" ⇒ 32
h ⇒ 104
e ⇒ 101
l ⇒ 108
p ⇒ 112
! ⇒ 33
On a donc notre message non crypté : 78 101 101 100 32 104 101 108 112 33
Afin de le crypter nous allons utiliser 2 opérations : La puissance et le modulo
Le modulo est le reste de la division euclidienne d'un nombre entier par un autre. Par exemple 19 modulo 3 = 1 car 19= 3*6 + 1, 30 modulo 4 = 2 car 30= 4*7 + 2; on le note ainsi : 30mod(4)=2
Rentrons dans le vif du sujet : pour crypter votre message vous devrez élever votre valeur de base à la puissance C puis avec la valeur obtenue la mettre au modulo N.
La clé publique est ( C , N ), ici ( 7 , 3239 ). Afin de crypter notre message l'opération sera donc :
Pour le "N" ⇒ (78ˆ7)mod(3239) = 631
Pour le "e" ⇒ (101ˆ7)mod(3239) = 2408
Pareil pour le 2ème "e" ⇒ 2408
Pour le "d" ⇒ (100ˆ7)mod(3239) = 2538
Et on continue de cette manière
"espace" ⇒ 2059
h ⇒ 1774
e ⇒ 2408
l ⇒ 2344
p ⇒ 2507
! ⇒ 1638
Le message codé est donc : 631 2408 2408 2538 2059 1774 2408 2344 2507 1638 et voilà, le message d'Alice est crypté, et plus personne ne peut le déchiffrer sans l'aide de la clé privée. Vous l'avez remarqué mais ici une lettre correspond à un chiffre ce qui est problématique car avec le calcul de fréquence d'apparition de chaque groupe on est en mesure de redonner à chaque groupe sa lettre d'origine. Il existe donc de petites techniques permettant de remedier à cela mais, pour rester au coeur du sujet nous ne nous y interresseront pas ici.
IV) Le déchiffrage :
Nous allons voir comment Bob devra faire pour déchiffrer le message d'Alice. Il a donc reçu ceci : 631 2408 2408 2538 2059 1774 2408 2344 2507 1638. Pour pouvoir retrouver le message d'origine Bob devra utiliser sa clé privée, ( 1783 , 3239 ). Ceci fonctionne de la même manière que pour coder mais avec les valeurs de la clé privée :
(631ˆ1783)mod(3239) = 78 ⇒ N
(2408ˆ1783)mod(3239) = 101 ⇒ e
(2408ˆ1783)mod(3239) = 101 ⇒ e
(2538ˆ1783)mod(3239) = 100 ⇒ d
(2059ˆ1783)mod(3239) = 32 ⇒ "espace"
(1774ˆ1783)mod(3239) = 104 ⇒ h
(2408ˆ1783)mod(3239) = 101 ⇒ e
(2344ˆ1783)mod(3239) = 108 ⇒ l
(2507ˆ1783)mod(3239) = 112 ⇒ p
(1638ˆ1783)mod(3239) = 33 ⇒ !
Bob retrouve bien le message d'Alice et peut voler à son secours sans que personne d'autre n'ait pu comprendre le message et soit averti de son arrivé imminente.
V) Comment réussit-on à retrouver le message d'origine ?
Comment se fait-il qu'avec tous ces calculs farfelus nous arrivions à crypter notre message puis à l'aide d'autres calculs à retrouver le message d'origine ? Cela est du à des théorèmes élaborés. Le cryptage asymétrique repose sur les fonctions à sens unique, c'est à dire des fonctions où calculer une image est simple mais retrouver son antécédent est bien plus compliqué. Un exemple simple est la multiplication de 2 nombres premiers (précisé dans le VI ). Mais tout ceci repose majoritairement sur le Petit théorème de Fermat créé en 1640 qui dit que si p est un nombre premier et a un entier non divisible par p alors :
Autrement dit a^(p-1) - 1 est divisible par p et n'a pas de reste
ex: 3^4 - 1= 240 qui est divisible par 5
Le but de cet article n'est pas de faire la démonstration du système RSA mais plutôt d'apprendre à l'utiliser nous ne pousserons donc pas plus loin cette analyse.
VI) Quelles sont les limites et les contraintes de ce système ?
Hélas ce système n'est pas infaillible... En réalité "infaillible" en cryptologie signifie plutôt "qui ne peut être déchiffré dans une période de temps suffisamment courte pour que le message ne soit plus obsolète". Effectivement, comme vous l'avez sûrement remarqué, on a dans la clé publique une partie de la clé privée. Cette partie là, 3239, dans notre exemple, est la base de ce système de cryptage. Alors la question que l'on se pose naturellement c'est pourquoi une telle information est à la vue de tous ? En réalité 3239 ne peut être utilisée toute seule. Il est nécessaire d'avoir les deux parties de la clé pour pouvoir déchiffrer le message.
Cependant, on peut retrouver la deuxième partie de la clé à partir de 3239. Le seul moyen est de retrouver les deux multiples de 3239. Etant donné que pour créer la clé privée, on utilise deux nombres premiers que l'on multiplie entre eux, nécessairement il n'existe pas d'autres nombres premiers qui multipliés entre eux donneraient aussi 3239. Il n'y a donc qu'une seule possiblité; Sans cela le cryptage asymétrique n'aurait plus vraiment d'intérêt.
Alors comment faire pour retrouver les deux multiples ? La seule solution qui existe est de tester toutes les multiplications entre des nombres premiers (à quelques approximations près mais c'est l'idée générale) ; Il n'existe pas encore d'autre méthode à ce jour.On voit assez vite la limite de la clé que nous avons créée pour ce TPE. Un ordinateur mettrait quelques secondes à briser notre code. En réalité, dans la vie de tous les jours le cryptage asymétrique est plutôt utilisé avec des clés de cette taille:
N=3107418240490043721350750035888567930037346022842727545720161948823206440518081504556346829671723286782437916272838033415471073108501919548529007337724822783525742386454014691736602477652346609
qui se décompose en :
P=1634733645809253848443133883865090859841783670033092312181110852389333100104508151212118167511579
et
Q=1900871281664822113126851573935413975471896789968515493666638539088027103802104498957191261465571
Il a fallu faire travailler 80 processeurs Opteron de 2.2GHz pendant 5 mois pour trouver P et Q. Autant dire que pendant une guerre il n'aurait servi à rien de tenter de le déchiffrer de cette manière.
Est-ce donc un moyen sûr ? Oui il l'est pour l'instant mais il comporte un problème majeur; L'envoi d'un message avec une clé sécurisée, donc longue, prend énormement de temps, bien plus qu'avec le cryptage symétrique. On l'utilise donc majoritairement pour envoyer la clé de cryptage symetrique (le cryptage symetrique utilise la même clé pour crypter et décrypter). Ainsi, on s'assure que cette clé ne soit pas trouvée puis on utilise le cryptage symétrique pour communiquer le message. En faisant cela on combine au mieux les deux techniques, ceci est appelé un cryptosystème hybride.
Cependant un adversaire majeur à cette technique se fait sentir de plus en plus : l'ordinateur quantique. Cet ordinateur ne fonctionne pas avec des transistors mais avec des qubits qui utilisent les propriétés de la physique quantique. Ces qubits ne prennent alors comme valeurs plus uniquement O ou 1 mais peuvent prendre aussi la valeur 0 et 1. C'est la superposition quantique qui ouvre de nombreuses portes à de nouveaux programmes, notamment de cryptanalise.

